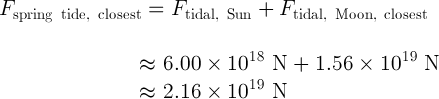Finally, for those of you who are afraid after the earthquake/tsunami

There is always great fear after a crisis, whether natural or man-made (as Americans found after 9/11). I think it is also natural for us to fall prey to the fantastic and dramatic; there is something special about feeling like we live in end times, or in a period of great peril.

But, time and again, history reminds us that it is not the doomsayers that make the greatest difference. It is the individuals, who carry their tiny parts of the world through a crisis through patience, balance of mind, and farsight. We may not know when the next earthquake happens - but we can and should do what we can to help those currently suffering, and looking for ways to better prepare for the inevitable.

That is the real work ahead, and that is where our energies and efforts should be focused.

The physics of the "Supermoon", part 2

In the last post, we used Newton's Law of Gravitation to calculate the relative strengths of the gravitational force on the surface of the Earth from (1) the Earth, (2) the Sun, (3) the Moon at closest approach, and (4) the Moon at its farthest distance from Earth. We also looked at the difference between (3) and (4), and argued that this is the important quantity when considering the impact of a "supermoon" compared with other times. The calculations were in the previous post, and summarized in a table, reproduced below:

In this post, we'll look at why the relative position of the Sun, Earth, and Moon influence tides, but the change in distance between the Earth and Moon is not as significant.

The "supermoon" on or about March 18 is occurring when the moon is in full phase, and at closest approach. This is shown in the figure below.

'

There are two configurations that create fairly strong tides. Spring tides, the strongest tides, occur when the Sun-Moon-and Earth are in a line, and in that order. 

The configuration above, which will occur around March 18, produces weaker tides, known as neap tides.

Tides occur because the Earth takes up a 3-dimensional space. Because one side of the Earth is a little bit closer to the Moon than the other side, that side experiences a slightly larger gravitational force. 

The force on the closer side of Earth is 

while the force on the far side of Earth is

Now, I'm using the mass of the Earth and treating it as if the entire Earth's mass is concentrated either in the near or far parts. This is incorrect. But since I'll be interested in only the relative strengths of these tidal forces, this is okay for now.

I first factor out the distance between the Earth and Moon of the denominator, and I remember that the radius of the Earth is much, much smaller than the distance between the Earth and the Moon. (The radius of the Earth is about 2% of the distance between the Earth and Moon). Therefore, I can approximate it using a Taylor (MacLauran) expansion (precalculus/calculus).

The tidal force is defined as the difference between the near side and far side forces. Therefore,

Simplifying, I get

Notice that it depends upon the distance to the third power. Therefore, tidal forces from far objects are much weaker than from nearby objects. 

Using a similar process, I can also get the tidal force due to the Sun:

Using the numbers summarized in the first table, I get the following values for the tidal force due to the Sun and the Moon:

I can now calculate the tidal force from the Sun and the Moon on the Earth in various configurations.

Let's go back to spring tides and neap tides. 

The strongest spring tide will occur when the Moon is closest to the Earth, 

The total tidal force in this case would be

The weakest spring tide will occur when the moon is farthest from the Earth.

In this case, the total tidal force would be

The strongest neap tide will occur when the moon is on the opposite side of the Earth relative to the Sun, but it is at the closest point in its orbit. (This is the configuration anticipated on Friday.)

In this case, the net tidal force is

Note: the minus sign only means that the net force is heading in the direction of the Moon, not the Sun.

The weakest neap tide occurs when the Moon is farthest from the Earth and on the opposite side of the Earth relative to the Sun:

In this case, the net force is

Here's a table summarizing the total tidal force in the four configurations of interest.

I scaled it to the weakest spring tide. Why did I do that? Because, every month, the Earth experiences a spring tide at least that strong. There is no reason, then, to freak out about a tide that is going to be less than or equal to half as strong as the tide experienced every new moon. 

In other words, don't freak out too much. There's nothing out of the ordinary with this configuration, either based on gravitational strength or on tides.

Additional notes:

Simplifications: I did not account for the relative inclination of the Moon relative to the Sun-Earth plane. Because the inclination is about 5 degrees, it will affect the results by at most a factor of 1-cos(5 degrees) ~ 0.004 = 0.4% for values involving the Moon. 

The physics of the "Supermoon", part 1

A LOT of my students are talking about the so-called "supermoon" that will happen on Friday. Basically, the Moon will be at perigee, or closest point to Earth in its orbit, and also in full moon phase.

In other words, the Sun, Earth, and Moon will be in the following position:

I'm not sure where the claim started, but someone is trying to convince the public that the world is going to end (or, at minimum, there will be some horrible earthquakes/tsunamis) around Friday.

Such a bold claim, especially one that comes on the heels of an absolutely horrible earthquake and tsunami in Japan, better be backed up by some outstanding evidence. Let's see what high school physics has to say.

Newton's Law of Universal Gravitation is

whereis the universal gravitational constant, m1 and m2 are the masses of the two objects, and d is the distance between them. This works just about anywhere in the universe, and definitely works for objects in our solar system.

[Note: The units are all SI. Newtons (N) are a unit of force; 1 N ~ 0.225 lbs.]

Think about the force on a single mass, say a person of mass mp = 100 kg, at the surface of the Earth. There are three significant gravitational forces acting on him: the forces of gravity between him and the Earth, between him and the Sun, and between him and the Moon.

The force of gravity between the Earth and that person (mp = 100 kg) is

where is the mass of the Earth, and the distance between the masses is the radius of the Earth, . Using these numbers, I get

The Earth's orbit around the Sun is nearly a circle, so I will treat the distance between the Sun and the Earth to be a constant. The force of gravity between the person on Earth's surface and the Sun is

where is the mass of the sun, and  is the distance between the Sun and the Earth. 

Again, using these numbers,

This is much smaller than the force of gravity from the Earth. (If it were larger, then we'd float off Earth's surface and eventually fall into the Sun.) 

What about the force of the Moon on the person? Because the moon has a more elliptical orbit, its distance from the Earth changes enough that it's worth checking the magnitude of the force when the Moon is closest to the Earth and when it is the farthest away. 

The force between the person on Earth's surface and the moon at its closest (as in the Moon's position around March 18) is

with is the mass of the moon, and  is the distance to the Moon when it is closest to Earth. [In astronomy, we call this lunar perigee.] Using these values, the force the Moon exerts on our person on Earth is

This is much smaller than even the force from the Sun. 

Now, the force exerted by the Moon on the person on Earth when the Moon is at its farthest distance is given by a nearly identical expression, where we replace the distance for closest approach with the greatest distance between the Earth and Moon: [Astronomers call this 

lunar apogee.]

Using the number for the mass of the Moon used in the previous calculation, we find

Note that this is, again, a very small number. Also note that the difference, 0.00372 N - 0.00297 N = 0.00075 N is a tiny, tiny fraction of the overall gravitational force on the person on Earth. Also note that this represents the maxiumum range of effect of the Moon's gravity on Earth. 

It's easier to consider the relative strengths of these in terms of percentages. So, I'm going to divide all the forces by the force on an object due to Earth's gravity, FEarth, and multiplying by 100 to get a percentage. 

The critical figure is the last one. The change in the gravitational force due to the change in the Moon's distance from Earth is a negligible factor.

But wait - you might be saying. What about tides? They exist, and they exist in part because of the Moon! Tune in to the next post for that.

Modeling the Sendai Tsunami

Today, I gave a brief lesson on the Richter Scale, earthquakes, and tsunamis. I initially made a pretty poor model (2-D) of the tsunami wavefront for my students in 3^rd period physics. By 7^th period physics, I had was using a crude 3-D cylindrical model, but unfortunately most students were tired and worried about the TOEFL test. So, here it is, reproduced for anyone curious how relatively simple math and physics can model a tsunami.

The 8.9 earthquake released approximately 1.41x 10^18 J (the equivalent of 336 megatons of TNT,about  7 times larger than the largest nuclear weapon ever tested).

Imagine all of that energy going into a cylindrical ring of water surrounding the impact. (This is really unrealistic - a lot would be lost into the Earth, or due to friction, or evaporation, or melting of rocks.) The outer edge of the wave is a cylinder of radius r (in km) and height h (in km). I’m estimating the shockwave to be roughly 1 km (just because I need a number to plug in – help from fluid engineers/hydrophysicists would be welcome!), which means that the inner cylinder has a radius of  r-1 and a height of h.

The volume of the outer cylinder is

And the volume of the inner cylinder is

Therefore, the volume of water (in km^3) in the expanding cylindrical ring is

The mass of water in that cylinder is simply the density of water times that volume of water.

Finally, assuming that the entire energy of the earthquake is transmitted into kinetic energy of the  water,

And the velocity of the water is

Now, in the deep ocean, h ~ 4km. Using this rough model, the velocity of the water with r=1 (just after the explosion) is about

The epicenter occurred about 80 miles east of Sendai (~130 km). Now, at a distance of r = 130 km, assuming the ocean remains the same depth, the velocity of the water would be

But near the coast, the water is actually much shallower. Using a more realistic depth, say about 30 meters (~100 feet), the velocity of the water should be

Remember – this is a very crude model. We ignore energy losses due to friction and phase changes or transmission into the Earth. But it captures the essential features of a tsunami:

1. The energy dissipates the further you go from the epicenter.

2.  However, shallower water means that the energy is spread across less mass, meaning that the water will actually have a high energy density at the shore.

Rocket Physics

I decided to write a note about this, partly because I didn't have a chance to explain a lot of this in class, and partly because some students not in physics may find this interesting.

Here's a video of the Apollo 11 launch, using a Saturn V rocket to boost Neil Armstrong, Buzz Aldrin, and Michael Collins into orbit around the Moon.

The formula for (non-relativistic) momentum is this:



In class, we discussed that our formula for impulse (change in momentum) is typically given as this:



But there is an assumption – this formula assumes that mass doesn’t change. In the case of a rocket, the mass does change. Technically, the formula for impulse should be:



(This is essentially cheap calculus – the only difference is that the capital delta will become a lowercase delta: d).

For this class, we can treat the exhaust velocity v as roughly constant, leaving us with this:



Now, let’s return to our definition of force as the ratio of impulse over a time interval:



Replacing the impulse with what we derived for a rocket,



This is our rocket equation. The force, or thrust, is equal to the rate of mass ejected from the rocket times the velocity of the ejected mass. This velocity is called the exhaust velocity.

The Saturn V rocket was the largest, most powerful rocket ever built by the United States. (It remains the largest and most powerful launch vehicle ever brought to operational status by height, weight, and payload.) It was made with one goal: to send American astronauts to the Moon.

Let’s now derive the acceleration at liftoff of the Saturn V rocket. (From Chapter 9: Linear Momentum and Collisions)

It had a mass of



or 2850 tonnes. Keep in mind that this rocket existed to send about 32 tonnes (the Lunar and the Command/Service modules) to lunar orbit. (Rockets are not really efficient.)

The rate of mass ejected per unit time was



Or 13.8 tonnes. This is about the mass of three elephants. So the Saturn V throws out three elephants worth of mass every second.

The exhaust velocity for a Saturn V was



This is actually faster than a speeding bullet (800-1500 m/s).

So, the thrust generated by the rocket would be



The mass of the Saturn V at launch was



Which means that the weight (gravitational force) would have been



Therefore, the net force on the rocket was



And the acceleration of the rocket at liftoff would have been



If you go back to the video of the Apollo 11 launch, you can see that the initial acceleration does, in fact, appear to be 2 m/s.

This is not much. Right at liftoff, an astronaut would feel a gentle tug – a feeling of being about 20% heavier. However, as the rocket lost mass, the acceleration would become greater, until the astronaut experienced several “gees”, or acceleration several times that due to surface gravity of the Earth. Astronauts therefore require excellent physical fitness to preserve their ability to function during liftoff and landing.

In class, I discussed the history of the modern rocket programs in China, the United States, and Germany. History is packed with examples of how choices and mistakes made by individuals and governments completely change the world.
Qian Xuesen, the father of the Chinese rocket program, was initially trained as an engineer focused on railroad administration. He was able to study mechanical engineering at MIT and learn about applied rocketry thanks to a Boxer Rebellion Indemnity Scholarship, a program created from surplus funds that were paid to the US by the defeated Qing empire. Qian was able to study at Caltech under von Karman and served as a commissioned colonel in the US Army Air Force. He worked with Von Karman to interrogate captured German scientists – Qian actually interrogated Wernher von Braun, who would later be influential in the US rocket program during the Cold War.

In 1949, allegations were made against him that he was a Communist, and he lost his security clearance. He was detained, and eventually placed in what amounted to house arrest. Eventually, he was traded to China for a dozen American fighter pilots captured during the Korean War. He went on to develop China’s rocket program and revamped Chinese education. He lived to see China launch an astronaut with its own rockets and return him safely to Earth.

I do not have time to tell you all the stories I have learned about the history of rocket and space programs in China, Germany, Russia, and the United States. But it is a field filled with people who were attracted by goals inspired, not coincidentally, by Jules Verne and visions of a distant future when humans would not be bound to the Earth of their ancestors. It was, by and large, a peaceful vision, one made more and more imperfect by the necessity to tie rocket development to military applications.

I leave you with a part of John Kennedy's Moon Speech at Rice University. Regardless of the many, many reasons America went to the moon, this serves as a reminder of why so many Americans contributed their genius and grit to such an amazing project, and what we can yet do, if our vision is clear, our minds well-stocked, and our spirits aflame.